La conversione tra massa e forza è un passaggio comune nella progettazione e nel dimensionamento dei sistemi di movimento lineare. Se sei fortunato, lavori principalmente in un insieme di unità: metriche o inglesi. Ma è probabile che ci sia stato (o ci sarà) un momento in cui è necessario lavorare in entrambi i sistemi di unità, possibilmente anche alternando unità inglesi per alcuni componenti e unità metriche per altri.
Se lavori nel mondo industriale, probabilmente incontri alcune misurazioni (come la lunghezza) abbastanza spesso in unità sia inglesi che metriche da poterle stimare con relativa facilità. Un metro è di circa trentanove pollici. Un pollice equivale a circa 2,5 centimetri …
Tuttavia, massa e forza sono una storia diversa. Parte della difficoltà nell’affrontare massa e forza, specialmente nelle unità inglesi, risiede nel fatto che definiamo il peso (forza) di un oggetto in libbre. Ma anche la massa è specificata in libbre.
L’uso di un’unità, la libbra, sia per la massa che per la forza è intrinsecamente fonte di confusione. Una variazione del sistema di unità inglese specifica la massa in termini di lumache, ma le lumache non sono certo un concetto comune. (Hai mai acquistato 0,1 lumache di mele?)
Per eliminare la confusione e dimostrare come convertire tra massa e forza, abbiamo messo insieme le seguenti formule per mostrare la relazione tra i due, sia in unità metriche che inglesi.
Massa e forza in unità metriche: kg e N
Esistono diverse varianti di quello che spesso chiamiamo il sistema di unità “metrico”, in cui le misurazioni sono basate su potenze di dieci. La versione più adottata del sistema metrico è il Sistema internazionale di unità (SI). Il sistema SI è a volte indicato come il sistema “MKS”, perché è l’unico sistema di unità che utilizza metri, chilogrammi e secondi come unità di base rispettivamente per lunghezza, massa e tempo. Si noti che SI è costituito solo da unità metriche, ma il sistema metrico contiene alcune unità che non sono incluse in SI. (Ad esempio, Celsius e litri sono unità metriche, ma non sono inclusi nel sistema SI).
Indipendentemente dalle unità di misura, la relazione tra massa e forza è data dalla seconda legge del moto di Newton , che afferma che la forza è uguale alla massa per l’accelerazione.
F = m * a
L’unità di massa tipica nel sistema metrico è il chilogrammo (kg), l’accelerazione è definita come metri al secondo quadrato (m / s 2 ) e l’unità di forza è il Newton (N), che è uguale a 1 kgm / i 2 .
Un Newton rappresenta la forza richiesta per accelerare 1 kg di massa a 1 m / s 2 .
F = kg * m / s 2 = N
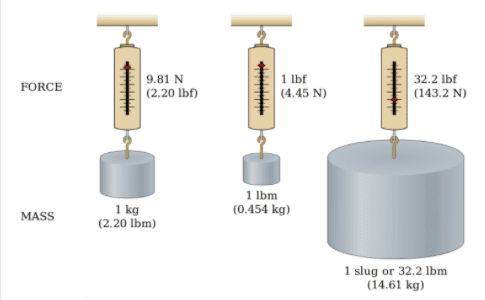
Quando applichiamo questa equazione in un’applicazione tipica, in cui l’accelerazione dovuta alla gravità è pari a circa 9,81 m / s 2 , troviamo che 1 kg di massa produce una forza (a volte indicata come “peso”) di 9,81 N.
F = m * a
F = 1 kg * 9,81 m / s 2
F = 9,81 N
Massa e forza in unità inglesi: lbm, slugs e lbf
Il sistema di unità inglese ha molte varianti, la maggior parte delle quali è stata a lungo scartata ad eccezione di una o due misurazioni che sono ancora in uso per applicazioni di nicchia. (Ad esempio, le unità degli speziali sono state per lo più sostituite, ad eccezione del grano.)
Attualmente, ci sono tre sistemi predominanti di unità inglesi: il sistema gravitazionale britannico (noto anche come sistema gravitazionale inglese), il sistema assoluto inglese e il sistema ingegneristico inglese. Per questa discussione, faremo riferimento ai sistemi di ingegneria gravitazionale britannica e inglese.
Nel sistema British Gravitational (BG), la massa è misurata in lumache, l’accelerazione è misurata in piedi al secondo quadrato (ft / s 2 ) e il prodotto di massa e accelerazione, forza, è misurato in libbre-forza (lbf) .
F = m * a
Una libbra-forza (lbf) rappresenta la forza richiesta per accelerare 1 slug di massa a 1 ft / s 2 .
F = lumaca * ft / s 2 = lbf
Quando applichiamo questa equazione in un’applicazione tipica, in cui l’accelerazione dovuta alla gravità è pari a circa 32,2 ft / s 2 , troviamo che 1 lumaca produce una forza (a volte indicata come “peso”) di 32,2 lbf.
F = m * a
F = 1 lumaca * 32,2 piedi / s 2
F = 32,2 lbf
Nel sistema di unità ingegneristico inglese , la seconda legge di Newton viene modificata per includere una costante gravitazionale, g c , che è uguale a 32,2 lbm-ft / lbf-s 2 .
In questo sistema, la massa è espressa in libbre-massa (lbm), l’accelerazione è espressa in piedi al secondo quadrato (ft / s 2 ) e la forza è espressa in libbre-forza (lbf). Per vedere perché è necessaria la costante gravitazionale, diamo un’occhiata alle unità dell’equazione della forza utilizzando il sistema EE:
F = m * a / g c
F = (lbm * ft / s 2 ) / (lbm-ft / lbf-s 2 ) = lbf
Si noti che la costante gravitazionale, g c , fornisce la coerenza nelle unità.
Quando applichiamo questa forma speciale della seconda legge di Newton a un’applicazione tipica con accelerazione dovuta alla gravità di circa 32,2 ft / s 2 , troviamo che 1 lbm produce una forza (o peso) di 1 lbf.
F = m * a / g c
F = 1 lbm * 32,2 piedi / s 2 / (32,2 lbm-piedi / lbf-s 2 )
F = 1 lbf
La cosa importante da notare qui è che per la maggior parte delle applicazioni (cioè quelle in cui la gravità è stimata a 32,2 piedi / s 2 ), si può presumere che una libbra-massa (lbm) abbia una forza (peso) di una libbra-forza (lbf ).