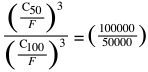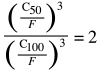Durante la selezione delle guide lineari, hai mai visto una dichiarazione di non responsabilità nel catalogo o sul sito Web del produttore per quanto riguarda le capacità di carico dinamico? In genere si legge qualcosa del genere:
Le capacità di carico dinamico si basano su 100.000 m di corsa. Quando si confrontano prodotti per i quali le capacità di carico si basano su 50.000 m di corsa, moltiplicare la valutazione di 100.000 m per 1,26.
Se hai visto questo, probabilmente ti sei chiesto da dove proviene l’1,26 e perché è importante. Per scoprirlo, esamineremo le equazioni della durata dei cuscinetti per ciascuna classificazione per ricavare il fattore di conversione. Ma prima, esaminiamo la differenza tra capacità di carico statica e dinamica.
La capacità di carico statico, secondo ISO 14728 Parte 2 relativa ai cuscinetti volventi , è la forza che provoca la deformazione permanente dell’elemento volvente (sfera) e della pista, che è pari a 0,0001 volte il diametro dell’elemento volvente. Questa è una specifica importante perché se viene superata, le caratteristiche di rotolamento del cuscinetto saranno compromesse. Tuttavia, la capacità di carico statico è valida solo quando il cuscinetto è fermo. Quindi, sebbene sia fondamentale considerare la capacità di carico statico nella selezione del cuscinetto lineare, è la capacità di carico dinamico che viene utilizzata per calcolare la durata del cuscinetto.
La capacità di carico dinamico è il carico al quale una guida lineare, con una certezza del 90%, raggiungerà la durata utile prevista prima che si verifichi la fatica (sfaldamento) sugli elementi volventi o sulle piste. La specifica ISO 14728 Parte 1 consente di utilizzare 50.000 mo 100.000 m come durata utile mirata per la capacità di carico dinamico. Pertanto, per fare un confronto tra guide lineari di diversi produttori, è necessario sapere se i loro coefficienti di carico dinamico si basano su 50.000 mo 100.000 m. È qui che il fattore di conversione 1,26 diventa importante.
Equazioni per il calcolo della durata dei cuscinetti lineari
Per iniziare, imposteremo le equazioni della durata dei cuscinetti per 50.000 m di vita utile e 100.000 m di vita utile:
Impostare le equazioni di vita uguali tra loro ci permette di iniziare a ricavare il rapporto tra C 50 e C 100 :
Spostare le variabili su un lato dell’equazione ci dà:
Che può essere semplificato in:
La forza applicata è la stessa per entrambi i calcoli di vita, quindi F può essere rimosso dal numeratore e dal denominatore, lasciandoci con:
Per eliminare il terzo potere sul lato sinistro, prenderemo la radice cubica di entrambi i lati:
Questo ci dà il rapporto che stiamo cercando:
In una forma più pratica, la capacità di carico di un cuscinetto basata su 100.000 m dovrebbe essere moltiplicata per 1,26 al fine di effettuare un confronto accurato con un cuscinetto lineare per il quale la capacità di carico è basata su 50.000 m:
E viceversa, la capacità di carico di un cuscinetto basata su 50.000 m dovrebbe essere divisa per 1,26 al fine di effettuare un confronto accurato con un cuscinetto per la quale la capacità di carico è basata su 100.000 m:
Come analogia, pensa a fare jogging con uno zaino pieno di pesi. Se stai facendo jogging per 10 miglia, potresti essere in grado di trasportare solo 20 libbre di pesi senza stancarti. Ma se fai jogging solo per 5 miglia, puoi facilmente trasportare 25 libbre di pesi senza fatica. Questo stesso principio è alla base della conversione tra capacità di carico basata su 100.000 m di vita e 50.000 m di vita.
Comprendendo la teoria alla base del fattore di conversione 1,26 e applicandola quando necessario, è possibile evitare il costo iniziale del sovradimensionamento dei cuscinetti lineari per la propria applicazione o il costo a lungo termine dei tempi di fermo e delle riparazioni dovuti al sottodimensionamento.